15. Mouse
and corns
In
the Indian temple the floor has rectangular form filled with identical square
tiles 1 × 1. Each tile contains from 0 to k (k
≤ 30000) corns. A mouse runs out from a left lower corner and go to the
exit in right upper corner.
Mouse
can go only right or forward, collecting all the corns from the tiles where it
resides.
Find
the route, where mouse can take as much corn as possible.
Input. The first line contains m and n (1 ≤ m, n
≤ 100) – the floor size. Next we have m
lines, starting from top, each contains n
numbers – the number of corns on the floor.
Output. Print the route of the mouse in format: RRFFFRF (F – step
forward, R – step right).
|
Sample input |
Sample output |
|
2 3 3 2 4 1 5 1 |
RFR |
SOLUTION
dynamic
programming
Algorithm
analysis
For the convenience of further calculations rotate the
board upside down. The vertical and horizontal tiles we count starting from 1. Then
the mouse route will run from the upper left corner – the tile with coordinates
(1, 1), into lower right corner – the tile with coordinates (m, n).
One step down the board will be encoded by the letter F.
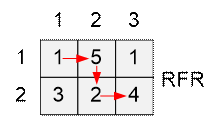
Tile with coordinates (i, j) contains a[i][j]
corns. Let res[i][j] contains maximum number of corns that
can be collected while moving from the upper left corner to the tile (i, j).
Into the tile (i, j) we can come either from (i – 1, j) or from (i, j – 1), so
res[i][j] = max(res[i – 1][j], res[i][j
– 1]) + a[i][j]
Its possible to avoid the array res, making
calculations in the array à. Let’s pass the floor tiles (array cells) from top
to bottom and left to right, assigning
à[i][j] = max(a[i – 1][j], a[i][j
– 1]) + a[i][j]
Initially, assign -1 to all cells of zero’s row and
zero’s column. However, for correct recalculation of value à[1][1] you need to
reset (assign to 0) of of the cells: a[0][1] or a[1][0]. In this case the new
value of à[1][1] becomes max(a[0][1], a[1][0]) + a[1][1] = 0 + a[1][1] =
a[1][1]. Further all the values à[i][j] will be calculated correctly.
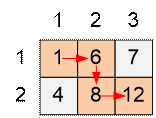
After the calculations a[i][j] will contain the
maximum number of corns that can be collected upon reaching tile (i, j).
The state of array à after the calculations looks like:
Algorithm
realization
Store the information about the number of corns in
array a. So on the tile with coordinates (i,
j) there is a[i][j] corns. The route of
mouse movements will be stored in array pos with the
length m + n – 1 (m and n are sizes of the floor).
#define MAX 102
int a[MAX][MAX];
char pos[2*MAX];
Read the input data. As the tiles can contain 0 corns,
initialize the array cells with -1. Rotate the board upside down.
scanf("%d %d",&m,&n);
memset(a,-1,sizeof(a));
for(i = 1; i <= m; i++)
for(j = 1; j <= n; j++)
scanf("%d",&a[m-i+1][j]);
Recalculate
the cells of array à so that à[i][j]
will contains the maximum number of corns that can be picked up upon reaching
the tile (i, j).
a[0][1] = 0;
for(i = 1; i <= m; i++)
for(j = 1; j <= n; j++)
a[i][j] = max(a[i-1][j],a[i][j-1]) + a[i][j];
Starting from the tile (i, j) = (m, n) we move to (1, 1) and
store the route of mouse movement into array pos. From the tile (i,
j) we should move into (i – 1, j) or into (i, j – 1) depending on which value a[i – 1][j] or a[i][j – 1] is greater.
i = m; j = n; ptr = 0;
while(i + j > 2)
{
if (a[i-1][j]
> a[i][j-1])
{
pos[ptr] = 'F';
i--;
}
else
{
pos[ptr] = 'R';
j--;
}
ptr++;
}
Print the route of mouse movement.
while(ptr--) printf("%c",pos[ptr]);
printf("\n");